In de kleuterklas zie je hoe kinderen zelf rekenkundige ervaring opdoen in het vormen van geometrische figuren met blokken, in het ordenen op kleur van schelpjes, het leggen op grootte van kastanjes en wat niet meer.

Die manier van leren rekenen vanuit eigen ervaringen is een vorm van modern rekenonderwijs dat perfect aansluit bij de uitgangspunten van de rekendidactiek in de Vrije School.

2.1. Alles op zijn plaats

Wezenlijk is dat de kinderen rekenhandelingen kunnen herhalen en zodoende

hun vaardigheden kunnen uitbreiden. Het is daarom van belang het zelfde rekenmateriaal vaker opnieuw te gebruiken en concrete rekensitituaties te ‘bewaren’.

De rekenkist biedt de mogelijkheid om allerlei ‘rekendingen’ op te bergen en structurerende mogelijkheden te bewaren

In die zin is de rekenkist een rekenkundige uitdaging op zichzelf: vakjes van verschillende grootte en vorm waarin je allerlei dingen kunt opbergen zoals kralen, damschijven, rekenkaartjes, steentjes of cocktailprikkers. Daarnaast is er plaats voor

rijggaren, of rekenspelletjes en zijn er enkele slimme voorzieningen aan de rekenkist aangebracht die het structureren ondersteunen.

In de rekenkist bergen de kinderen van alles op wat ze zelf verzameld hebben bij het verkennen van de eerste rekenervaringen; later zijn dat ook de materialen waar een kind behoefte aan heeft als het rekenend bezig is, dat kan van alles zijn en voor elk kind verschillen.

De rekenkist is bedoeld als instrument dat kinderen stimuleert om van het handelingsniveau op een natuurlijke wijze over te stappen op een meer mentaal rekenniveau.

Concrete rekenhandelingen, waarbij kinderen hun eigen rekenwereldje creëren, gaan gepaard met ordenen, tellen en structureren. Wanneer kinderen zelf hun materialen maken, tekenen zij bij voorbeeld mooie getalkaartjes, leggen hoeveelheden schelpjes in bijzondere patronen, rijgen eigen rekenkettingen, of bedenken zelf rekenspelletjes met materiaal uit de natuur of spullen die al in de kist aanwezig zijn. Door alles wat er in de

rekenkist bewaard kan worden, door de structurerende mogelijkheden die de rekenkist biedt, worden de kinderen zelf tot rekenen geactiveerd.

Ook leerlingen die het rekenen niet zo makkelijk afgaat, worden actief bij het

rekenen in de klas betrokken. Rekenen wordt daarmee geen abstracte, betekenisloze activiteit waar kinderen niet de zin van zien en zich niet mee kunnen verbinden.

3 Suggesties voor het gebruik van de rekenkist.

3.1. Ook voor kleuters

De rekenkist laat zoveel ruimte aan de gebruiker – kind en leerkracht – dat het voor de hand ligt dat ook oudste kleuters er mee kunnen spelen en werken. Vooral in vormen van kleuteronderwijs zoals de poortklas of de voorjaarsklas is de rekenkist een prachtige mogelijkheid om structuur aan te brengen in de rekenervaringen zonder dat rekenen hoe dan ook abstract wordt. Dan bewaar je in de rekenkist:

- allerhande kleine dingen zoals schelpjes meegenomen van vakantie, of eikels geraapt op weg van huis naar school;

- de eigen memoriekaartjes die samen met de leerkracht gemaakt zijn;

- de dobbelstenen die je gebruikt bij een bordspel;

- de steentjes die je gekregen hebt toen je voor je 6e verjaardag in de klassen ging trakteren;

- de fiches die je kunt gebruiken bij bordspelen;

- dingen die kinderen sparen.

Het bijzondere wat de rekenkist toevoegt is dat de schoolrijp wordende kleuter zijn eigen materiaal krijgt. Naast het spelen met het klassenmateriaal heeft het kind nu ook zijn eigen dingen. Dat dit in een doos kan, dat daar een deksel op hoort is een natuurlijke stap naar individualisering: Ik bewaar voor mezelf hoe ik de dingen doe.

Voor zover materiaal uit zichzelf tot spelen en verkennen uitnodigt hoeft de leerkracht daar geen aanwijzingen bij te geven.

Dat geldt voor memoriekaartjes of dobbelstenen. Maar er kan ook een spel in dat enige

uitleg behoeft maar daarna ook vrij door de kinderen gespeeld wordt zoals de luciferrace:

Voor in de rekenkist maak je lucifers van gelijke lengte (afgebrand en schoongemaakt – of met één kant gekleurd). Op een dobbelsteen zijn de ogen met een etiketje afgeplakt. De dobbelsteen geeft de volgende bewegingen aan:

- rechts = geel + r

- links = blauw + l

- 1 vooruit = rood met 1 streepje

- 2 vooruit = rood met 2 streepjes

- achteruit = groen met 1 streepje

- beurt overslaan = wit

Voor dit spel zijn voor ieder kind nog een links- en rechts button nodig.

Zelfde kleur en letter als op de dobbelsteen. Spelvarianten:

Kind alleen:

- Werpen met de dobbelsteen en lucifers leggen bijvoorbeeld tot aan de rand van de tafel;

Twee kinderen:

- Naast elkaar: wie is het eerst aan de overkant;

- Naast elkaar: wie heeft de meeste lucifers voor hij bij de rand is;

- Tegenover elkaar: idem

- Tegenover elkaar: wat doe je als je in elkaars parcours komt?

Daarnaast kan een leerkracht opdrachten geven met materiaal zoals:

- Leg je schelpjes eens neer op kleur of grootte;

- Zoek soort bij soort;

- Leg eens figuren van je steentjes;

- Kun je figuren van steentjes herhalen – hoeveel dezelfde figuren kun je maken. Heb je steentjes over?

- Kun je de figuren natekenen?

- Kun je met steentjes een figuur spiegelen t.o.v. een spiegellijn?

- Kun je de figuren ook natekenen?

3.2 Van eigen spulletjes naar bijgeleverde materialen

De rekenkist is in verschillende vakjes verdeeld en is aanvankelijk nog leeg.

Hij raakt in de loop van de tijd geleidelijk gevuld. Hierboven werd al duidelijk wat er zoal in de rekenkist kan worden opgeborgen. Dat kan allerlei zijn. Allereerst dat wat de kinderen zelf verzamelen.

Veelzijdig materiaal waarmee ze zelf aan de slag zijn gegaan bij het rekenen:

knikkers waarmee ze in de pauze op het schoolplein spelen; dingetjes die ze er ruilen. Het kan dus evenzeer om kleine spullen uit de rage van de dag gaan zoals buttons en plaatjes, speeltjes of stikkers. De leerkracht zal daarin de kinderen stimuleren of beperken, al naar gelang hij of zij de dingen bruikbaar vindt in de klas.

Al die hoeveelheden die zich laten ordenen en tellen kunnen de kinderen gebruiken om er structuren en waarde aan toe te kennen. Dat is bij uitstek adaptief onderwijs, waarbij wordt uitgegaan van de eigen rekenactiviteit van de kinderen.

Met de rekendoos op tafel krijgen de kinderen de opdracht bijvoorbeeld

- leg eens 3 dezelfde dingen neer

- leg eens 2 grote en 2 kleine dingen naast elkaar

- leg eens 3 verschillende dingen neer

- leg eens 3 verschillende dingen neer, maar dan van elk 2 stuks.

Maar ook een kind kan zulke opdrachten geven aan de klas of een groepje.

Naast de dingen die de kinderen zelf in de doos kunnen verzamelen wordt

er ook speciaal materiaal bijgeleverd:

- Rekendamschijven

- Rekenstaafjes

- Rijgkralen

- Kralen rood/blauw voor het rekenrek-snoer

- Blanco kaartjes

- Stuk elastiek om te rijgen

- Lapje om dingen onder te leggen

- Rijggarnitiuur om kralen te rijgen

- Dobbelstenen

3.2.1 Het doekje

dat bij de rekenkist hoort kan gebruikt worden voor opdrachten als:

- Pak eens 9 schijfjes uit en maak daar (twee) groepjes van. Leg ze onder het doekje en laat een ander kind door het doekje voelen hoeveel er in elk groepje zitten.

- Dat kind kan zeggen wat het voelt, maar kan ook met de eigen schijfjes neerleggen wat er onder het doekje ligt. Doekje weg en vergelijken!

- Maar het andere kind kan het bijvoorbeeld ook tekenen op een blaadje.

3.2.2 De blanco kaartjes

kunnen de kinderen gebruiken om daar op te tekenen of te schrijven.

Zo kunnen er kaartjes gemaakt worden met de tekening van de getalkwaliteit zoals:

- één: de zon

- twee: zon en maan

- drie: het stoplicht

- vier: de 4 poten van de stoel

- vijf: de vijfster uit het appelklokhuis

- enz.

Als er op andere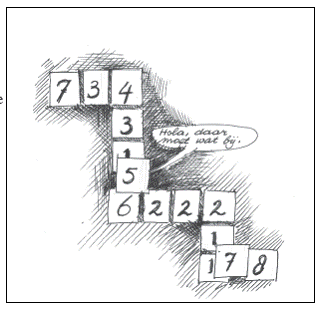 kaartjes de getallen

worden geschreven –

Romeins of in gewone cijfers al naar de klas gewend is – kunnen getalbeeld en

cijferbeeld samen gelegd worden.

Maar deze paren kaartjes lenen zich ook uitstekend voor een memoriespelletje

met je buurvrouw.

Als je veel kaartjes met getallen hebt kun je er samen met een ander kind een getalparcours mee leggen. Eén kind legt de 7 neer; de ander mag aansluiten

met getallen die samen ook 7 zijn zoals de 3 en de 4. Nu past de ander bij de

4 aan met de getallen: 3 en 1. Hola! Je kunt niet verder. Maar als je een kaartje

half op de ander legt moet je buurman die twee optellen: 5 er op en de

ander sluit aan met 6 …..

Wedstrijdje? Wie zijn kaartje tegen de rand van de tafel aan kan leggen heeft

gewonnen. En de spelregels? Die kun je toch samen wel bedenken!

Maar je kunt op de kaartjes ook getallen in een (meetkundige) structuur,

een patroon, of een bijzondere vorm laten tekenen door de kinderen.

Op die manier representeren de kinderen een getal - of een aspect er van-

Dan is tellen daarbij niet meer nodig. Kinderen bedenken vaak zelf zulke

‘symbolen’; en binnen zo’n beeld zien ze weer extra structuren zoals de 6

stippen van de dobbelsteen als dubbel.

Getallen krijgen betekenis, worden ‘sprekend’, als ze zo ‘gebruikt’ zijn.

3.2.3 De dobbelstenen

kun je natuurlijk gebruiken bij een zelfgemaakt ganzenbordspel, maar er zijn ook andere spelletjes mee te doen zoals:

vakken vullen: de kinderen werpen met 2 dobbelstenen. Alleen wie dubbel gooit mag de hoeveelheid in een ruitveld leggen, Dat veld kan de leerkracht maken, maar kinderen kunnen het bijvoorbeeld ook zelf vouwen/tekenen.

Wie het eerste zijn veld vol gelegd heeft is de winnaar.

Ook hier kunnen in plaats van cijfers kleine getalprentjes op de dobbelstenen geplakt worden – kleine plakrondjes of etiketjes zijn daar heel geschikt voor.

Er zitten dus ook dobbelstenen in, verschillend van vorm.

Behalve de kubus (het 6 vlak), een 4-, 8-, 12-, 20- en 2x een 10-vlak, met daarop verschillende getallen.

Dobbelstenen lenen zich voor talrijke (reken) spelletjes.

Met de verschillende soorten stenen kun je heel goed differentiëren.

Op plakrondjes zijn bovendien nog andere getallen aan te brengen.

Naast de gebruikelijke symbolen en getalbeelden (onder andere de bekende

stippatronen) leren kinderen zo de gewone getalrij kennen, maar ook bijvoorbeeld de tafelrij van 2.

Dobbel-jatzee:

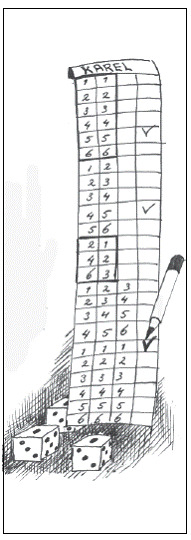
In een groep 4 ontwikkelden de kinderen

dit Jatzee-spel. De regels die ze erbij

maakten luidden:

Er wordt geworpen met 3 stenen, want

anders gooi je te vaak niets.

Het bovenste vak met de 2-tallen moet

geheel gevuld worden. Bij iedere bruikbare

worp mag je een fiche op het achterstaande

vakje leggen.

In het onderste vak staan de superworpen:

3 x hetzelfde of 3 opeenvolgende

getallen.

Als je die gooit mag je ze invullen.

Als één speler het bovenste vak gevuld

heeft is het spel afgelopen. De score

wordt voor iedere speler berekend aan

het aantal fiches in het onderste vak. Zijn

er in het bovenste vak nog plaatsen open

dan moeten die eerst met deze fiches gevuld

worden.

Wie de meeste fiches uit het onderste vak

heeft overgehouden is de winnaar.

Natuurlijk zijn er allerlei andere yahtzeevormen mogelijk die eenvoudiger zijn. Er kan bijvoorbeeld ook gewerkt worden met de afbeeldingen van de dobbelstenen in de lijst.

Als je dit spel in groepen speelt kun je per groep een spelleider aanstellen die ook kijkt of kinderen geen mogelijkheden over het hoofd zien. Een slimme leerling doet dat graag.

Dobbelstenen lenen zich dus voor talrijke (reken) spelletjes, met de verschillende stenen is daarbij differentiatie mogelijk. Op plakrondjes zijn bovendien nog andere getallen aan te brengen.

Naast de gebruikelijke symbolen en getalbeelden (onder andere de bekende

stippatronen) leren kinderen zo ook getalrijen kennen en hanteren. De gewone telrij natuurlijk, maar bijvoorbeeld ook de rij van de (on)even getallen (de ‘dubbel’ of ‘eerlijk verdeel’ getallen, en zo de tafel-rij van 2).

Later volgen weer andere (tafel)rijen, de tiental-rij om het gebied tot 100 te verkennen; een verdubbelingsrij, die steun geeft bij vermenigvuldigen en delen uit het hoofd; en

natuurlijk zaken waar leerlingen zelf mee komen.

“Welke groep heeft als eerste de 2, 4, 8, 16, 32, 64 rij geworpen?”

Of “Wie komt (met een 12 vlaks dobbelsteen) het verst in de rij van 7 voor de zandloper leeg is?” (Zo krijgen ze niet alleen zicht op die rij, maar ook gevoel voor ‘hoe lang iets duurt’.)

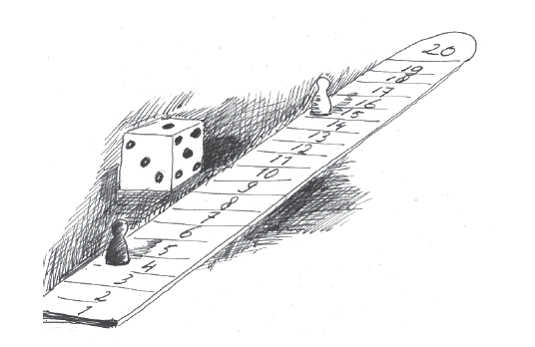
Ook een klein bordspel is in de kist te bewaren. Zoals ‘Ladder op en af ’, dat met één dobbelsteen en één pion gespeeld wordt op een getekende ladder van 20 treden.

“Steeds vertellen wat je daarbij denkt; en aan het eind van een uitgespeeld spel de pion weer op de 10e sport zetten”.

Carla, die het vorige spel verloor, mag nu als eerste dobbelen, ze gooit 4.

De pion schuift van de 10e naar de 14e tree. Nu is Jan aan de beurt, die werpt 6.

Dat is lastig, ‘14 eraf 6’, uit het hoofd lukt nog niet in een keer: hij telt 6 terug en komt zo op 8.

‘Kun je zo zien’, zegt Carla: 6 dat is 2 meer dan 4, je moet gewoon 2 omlaag vanaf 10 waar ik eerst stond.’.

Nu is zij weer aan de beurt. Ze gooit een 3. ‘Dat is dan 11’ laat Jan vervolgens van zich horen.

‘Dat wist ik ook wel hoor’, komt meteen de repliek.

Wie gaat er winnen? Jan die als eerste op de grond, bij 0 de ladder verlaat, of Carla doordat ze bij 20 met de pion eerder de bovenkant van de ladder bereikt?

3.2.4 Het deksel van de kist

Het schuifdeksel van de rekenkist is een handig didactisch hulpje voor het rekenen.

De kinderen kunnen met een elastiek zelf een rekensnoer rijgen dat op het deksel een praktisch rekenrek (zie paragraaf 3.5 ) wordt:

Aan de andere kant van het deksel zijn houten randjes aangebracht waarop de kinderen met hun spulletjes of zelf gemaakte getalkaartjes hun ‘rekensommetjes’ kunnen neerleggen.

Bij de rekenkist hoort ook een schoolbordje waar de kinderen de getalrelaties

(sommetjes) die ze hebben ontdekt kunnen tekenen of schrijven.

Ze kunnen dat met het bijgeleverde krijtje doen, maar ook even vlug met een natte vinger. En met het sponsje dat bij de kist zit, kun je het bordje weer helemaal schoon vegen.

Van de didactische mogelijkheden van de rekenkist ziet u in de volgende

hoofdstukken enkele voorbeelden.

4. HET DIDACTISCHE MATERIAAL

4.1 De vakverdeling van de rekenkist

Als het deksel van de rekenkist wordt afgeschoven zie je hoe de kist is verdeeld in vakjes van verschillende grootte.

Die vakjes – bedoeld om alle spulletjes handig op te bergen – nodigen ook uit tot allerlei sorteeractiviteiten.

Als de kinderen met een bepaalde hoeveelheid kastanjes of kralen aan de slag gaan zullen er kinderen zijn die in elk vakje evenveel doen; anderen sorteren op grootte of kleur. Weer anderen vullen de vakjes en merken dat er vakken leeg blijven. Tussen de kinderen kan er een levendige uitwisseling ontstaan over de manieren waarop je in de vakjes de dingen kunt verdelen.

Waarnemen hoe kinderen tot verdeling komen vanuit eigen maatstaven of hoe ze elkaar manieren van verdelen aanreiken biedt de leraar een schat van informatie waar hij in de rekenwiskundeles op aan kan sluiten.

De concrete situatie kan door de kinderen ook afgebeeld worden.

Door sommige kinderen nog heel direct, door in de vakjes kaartjes te leggen met het aantal kastanjes of kralen er op geschreven. Anderen zullen hun verdeling schematisch op papier afbeelden.

Natuurlijke materialen lokken benoemde getallen uit. De kleine kastanjes gaan in het ene en de grote in een ander vakje. Blijken dit er na telling 5 en 2 te zijn dan horen die aantallen bij deze groepjes kastanjes. Later, als ze vaker structureren met de rekenstaafjes of damschijven die beide identiek van vorm zijn, is er sprake van aantallen zonder meer.

Omdat deze voorwerpen onderling niet verschillen, zijn alle hoeveelheden dan met onbenoemde getallen weer te geven. Wie onbenoemde hoeveelheden wil (be)schrijven heeft behoefte aan symbolen, aan cijfers.

De leraar kan aan die behoefte tegemoet komen door op zeker moment de cijfers

te introduceren. De didactiek achter de rekenkist kiest er voor om die behoefte in de kinderen te wekken en hen zelf te laten ontdekken hoe je cijfers kunt gebruiken.

4.2. De rekenstaafjes

Bij de rekenkist worden korte houten staafjes geleverd die in de gaatjes aan de onderkant van het deksel geplaatst kunnen worden. Die gaatjes zijn aangebracht in de structuur van het rekenrek. Op die wijze kunnen ze ook gebruikt worden.

In tegenstelling tot het rekenrek kunnen de kinderen iedere hoeveelheid staafjes tot 20 gebruiken en blijft er geen ‘rest’ over zoals bij het rekenrek als je met getallen kleiner dan 20 werkt.

De rekenstaafjes zijn in twee kleuren geschilderd: de ene helft rood, de andere blauw.

Als ze in een gaatje geplaatst worden steekt er één kleur naar boven. Door het staafje om te draaien kun je van rood naar blauw en omgekeerd wisselen.

De kinderen kunnen ze gebruiken om er aardige patronen mee te leggen, maar ze kunnen ook specifiek gebruikt worden bij optellen en aftrekken.

In hoofdstuk vier ‘Optellen en aftrekken met het rekenrek’ wordt

daar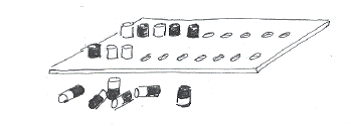

nader op ingegaan.

De kinderen kunnen door de vormgeving van de staafjes de structuur van een bepaalde hoeveelheid staafjes veranderen zonder het totale aantal te wijzigen. Het is een heel aardige manier om een hoeveelheid in twee groepen te splitsten.

De ‘vijfstructuur’ van de gaatjes in het deksel van de rekenkist brengt de kinderen ertoe om zich getallen vanuit een vijfstructuur voor te stellen, zodat deze structuur als denkmodel voor de kinderen ter beschikking komt.

4.3 De damschijven

De damschijven hebben hun plaats in de rekenkist gekregen op praktische gronden.

Veel los rekenmateriaal dat kinderen zelf verzamelen is in het gebruik vaak minder praktisch. Boontjes of eikeltjes rollen gemakkelijk van tafel, ook als er een lap gebruikt wordt om op te werken. Kastanjes zijn handig omdat ze mooi van omvang zijn en makkelijk op te pakken, maar ze kunnen onderling sterk van grootte verschillen. Sommig materiaal laat de kinderen te weinig vrij, hoe mooi het ook is: kleine minerale steentjes zijn prachtig om te zien, maar scheppen een twijfelachtig didactisch uitgangspunt:

Wat nemen de kinderen waar en waarmee verbinden ze zich?

Met de rekenkundige vraagstelling of met de mooie kleurtjes van de stenen?

Daarom is het goed om ook neutraal en handzaam materiaal ter beschikking te hebben.

De damstenen voldoen aan die criteria: ze zijn gelijkvormig, bruikbaar van omvang en liggen stevig op het tafelblad. Ze laten zich gemakkelijk schuiven als het kind groepjes maakt.

Opdrachten die met damstenen gegeven kunnen worden zijn bijvoorbeeld eenvoudige verdeelopdrachten op een groot werkblad van A3 formaat.

Aan de brede kant zijn twee rijen van 20 hokjes getekend.

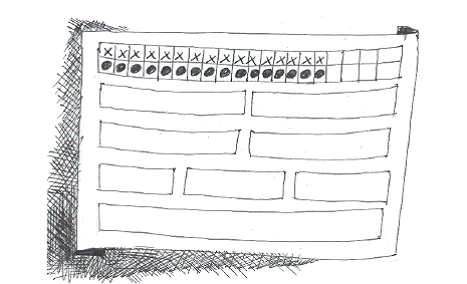
In de onderste rij kunnen de kinderen damstenen leggen. De hokjes daarboven kunnen

de kinderen inkleuren of intekenen. De damstenen kunnen nu verdeeld worden over de kaders. Door de ingekleurde hokjes wordt de hoeveelheid voor de kinderen bewaard ook als er met de stenen geschoven wordt.

Zo’n werkblad kan door de leraar voorbereid en gekopieerd worden, maar kan ook door de kinderen zelf gemaakt worden.

Er zijn allerlei variaties denkbaar in vormgeving en opzet. De kinderen kunnen als ze een nieuwe verdeling maken de hoeveelheden in het vak noteren voor ze de damstenen verschuiven.

4.4 De kralen en de snoeren.

Met verschillende natuurlijke materialen zijn er al in de kleuterklas allerlei kettingen geregen. Jonge kinderen, eenmaal hierop geattendeerd rijgen graag mooie patronen. Later kunnen die de rijen uit het ritmische rekenen verbeelden.

In de rekenkist zitten 4 soorten kralen. De kinderen kunnen zelf bedenken in welke patronen ze de kralen aan het snoer rijgen.

Samen met de klas kan gekeken worden hoe ieder kind zijn ketting geregen heeft.

Het helpt de kinderen om over aantallen en structuren te praten in een ‘rekengesprek’.

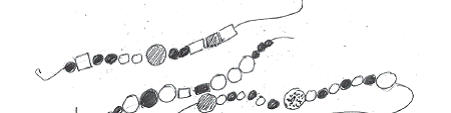
De kinderen kunnen hun kettingen ook natekenen en zo een concrete situatie leren afbeelden.

Het zijn belangrijke rekenstappen die ook met oudste kleuters heel goed genomen kunnen worden.

De situatie kan natuurlijk ook omgekeerd worden als de kinderen na wat ervaring opgedaan te hebben met de kralenketting nu éérst een ontwerp maken op papier en dat dan in de praktijk uitvoeren. Kinderen kunnen ontwerpen voor elkaar maken en voor de bollebozen kan de opdracht uitgebreid worden door een extra rijgopdracht zoals het werken met vooraf gegeven hoeveelheden; het maken symmetrische kettingen of het

werken met bijvoorbeeld 2 rijgpatronen.

4.5 De bijzonder kettingen: het 20-snoer

en het 100 snoer

Het 20-snoer

Het ‘20 snoer’ is een bijzondere ketting die bestaat uit 2 maal 5 rode en 2 maal 5 blauwe kralen, op het elastieken snoer geregen in een dubbele 5-structuur.

Het 20-snoer is ook op de achterkant van de deksel boven de rekenholletjes te spannen via de hierin aangebrachte inkepingen.

De kralen vormen dan samen het ‘rekenrek’. Links zitten de knoopjes achter het plankje, rechts is dat een lusje, gevormd tussen de 10e en 11e kraal.

Zichtbaar voor het plankje zitten er dan twee keer 10 kralen onder elkaar, steeds 5 rode en 5 blauwe op rij, schuift men er enkele opzij, kan er tussen de kralen een opening ontstaan.

Met dit rekenrek zijn getallen tot 20 dus op twee manieren aan te geven:

Of als lijn model op rij, ’10 kralen boven en nog 4 op de onderste rij’ staan dan voor het getal ‘14’.

Ofwel als groepjes model in een dubbelstructuur, dus ‘14’ als ‘dubbel 7’, en - lettend op kleur - als ‘dubbel 5 en dubbel 2’. Want de met kleur aangegeven ‘groepjes van 5’ maken tellen overbodig. Immers zonder tellen is door kinderen slechts het aantal van ten hoogste 3 te herkennen, hier echter is door de kleurstelling ook het aantal 5 in één blik te

overzien. En 4 wordt zo tot het ‘bijna 5’ getal.

De kinderen kunnen ontdekken dat er ‘dubbele getallen’ zijn en getallen die steeds 1 meer dan dubbel zijn:

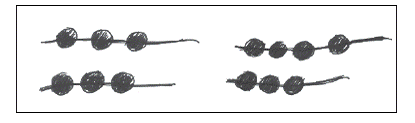
Bijvoorbeeld: ‘7’, als ‘dubbel 3 en 1’, of als ‘1 minder dan dubbel 4’. In dit

structureren komt zo ‘rekenen’ als vermeerderen/verminderen per één in beeld.

In zulke visuele structuren kunnen aantallen nu benoemd en gememoriseerd

worden.

Het 100-snoer

De rekenkist bevat ook kleine kraaltjes (in twee kleuren) waarmee grote aantallen in porties (onder andere groepjes van 10) te verdelen zijn.

De leraar legt een flinke hoeveelheid kraaltjes in twee kleuren op een lap.

De kinderen mogen schatten hoeveel het er wel zijn. Enkele kinderen mogen hun schatting toelichten. Dan schrijven de kinderen hun schatting op een papiertje. Als de klas verder aan het werk gaat, mag één kind de kralen aan een snoer rijgen.

Telkens in groepjes van 10 in één kleur. Als er geen 10-tallen meer te rijgen zijn wordt er een knijpertje op het snoer gezet. Hierachter worden de overgebleven kralen geregen.

Nu kan de hoeveelheid geteld worden in groepjes van 10 en aantal losse kralen.

Bij de volgende schatting is er een kind dat vraagt of hij de kralen op de lap in groepjes mag leggen. Hij maakt handig groepjes die op het oog 10 kralen groot zijn.

‘Het zijn er ongeveer 10 – 20 – 30 – 40 - 50 – 60 – 70 …’, zegt hij.

Met de kleine kralen kan ook een specifieke 100-ketting geregen worden.

Telkens om en om 10 kralen van een kleur. Daarmee leert het kind rekenen in het gebied tot en met 100 op basis van het volgorde principe. Het legt de relatie tot de decimale schrijfwijze van de getallen.

Zo leidt de 100-ketting tot het later te gebruiken model van de ingevulde en open getallenlijn. De kinderen kunnen met de 100-ketting de G-10 methode verkennen: uitgangsgetal G heel laten, dan de 10-tallen erbij of eraf en tenslotte de eenheden.

De kinderen kunnen ontdekken dat je de opdracht: 23 erbij 36 uitvoert met de 100-ketting door eerst 23 kralen af te tellen (in de structuur van de ketting 10-10-3) en dat aantal met een knijpertje te markeren; dan 3 maal een 10-tal erbij, ook gemarkeerd door een knijpertje en tenslotte de 6 erbij te tellen: laatste knijpertje achter het ‘antwoord’: 59.

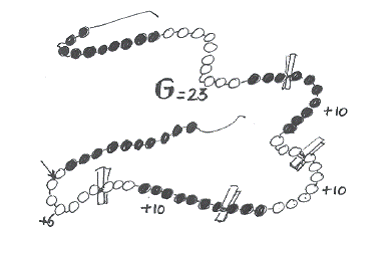
Als de leerling de opdracht op de 100-ketting heeft uitgewerkt kan hij aanwijzen

en zeggen:

23 􀃆 33 􀃆 43 􀃆 53 􀃆 59.

Omdat de 100-ketting met de 10-structuur werkt en niet met de 5 structuur van het rekenrek verdient het aanbeveling om aanvankelijk met begingetallen te werken die ten hoogste 3 ‘kralen’ van het tiental afliggen.

De kinderen kunnen de vervolgstappen in één keer overzien: tiental + 3.

Ook de aftrekking verloopt op dezelfde wijze, maar nu terugtellend.

Voordeel van de G-10 methode waarbij het begingetal heel blijft, is dat er geen delen van dit gesplitste getal onthouden moeten worden.

Een meisje rekent uit 43 eraf 26. Ze denkt even na en geeft als antwoord: ‘11’.

Leg eens uit zegt juf. ’40 – 20 is 20, dan nog 6 eraf dat is 14 en dan nog de 3 eraf , dat is 11.’

‘Maar’, zegt juf, ‘je hebt eerst de 3 van de 43 afgehaald, die moet je er dan weer bij optellen’. Het meisje zucht: ‘Maar het is toch een min-som?’

Nu zou de leerkracht de 100-ketting bij de hand moeten hebben om te laten zien dat je beter de 43 heel kunt houden. Dan heb je niet het onthoudprobleem en de vraag: moet die laatste hoeveelheid er nu bij of af ?

Deze rekensnoeren bereiden dus heel concreet voor op het rekenen, eerst tot 20 en later tot 100.

We noemen dit materiaal hier ‘lichaamsverlengend’ omdat het een brug slaat tussen tellend rekenen en mentaal rekenen. Het eerste doen kinderen veelal op de vingers of in combinatie daarmee.

Mentaal rekenen echter doen ze op basis van abstracte getallen en relaties daartussen.

4.6 De didactische hoofdroute

De grondgedachte achter de rekenkist is dat de kinderen eerst concreet werken en dan

in voorstellingen via ‘modellen VAN’ naar ‘modellen VOOR’, tot de rekenprocessen zich

uiteindelijk mentaal voltrekken.

Deze stelling moge de didactische hoofdroute van het leren rekenen verwoorden,

maar niet bij alle kinderen voltrekt zich het leerproces langs deze didactische route.

Er zijn bijvoorbeeld kinderen die moeiteloos mentaal rekenen maar zich daarbij niets weten voor te stellen. Voor hen kan dit materiaal het rekenen weer ‘in de wereld’ plaatsen, zij bewandelen dan dezelfde leerroute in de andere richting: van mentaal proces naar concrete handeling.

Belangrijk is dat kinderen niet alleen met deze materialen manipuleren, maar hun vondsten ook uitwisselen en er samen over praten. Zo wordt verwoord en dus gedacht wat gedaan en gezien is. Een kind dat voor getallen tot tenminste10 beschikt over ‘denkbeelden’ of anders gezegd getalbeelden, zal bij het rekenen niet voortdurend alles (her)tellen. Getallen zijn dan zowel te kennen als een te tellen aantal, maar ook te denken via één of meer (meetkundige) structuren. In zulke structuren is het tellend

rekenen vervangen door structurerend rekenen.

Antwoorden op rekenvragen zijn zo ook op andere wijze dan tellend te vinden.

5. Optellen en aftrekken met het rekenrek

Getalbeelden van de getallen onder de 10 hebben de kinderen geoefend op het plankje uit de rekenkist, eerst met de losse staafjes in de gaatjes, waarbij de kinderen zelf allerlei patronen uitprobeerden.

Met 9 werden er bijvoorbeeld - blauw en rood om en om – tellend 5 blauwe en 4 rode in de holletjes gezet.

Als de leerkracht de kinderen zo ziet verdelen zegt ze: ‘Zet nu eens alle blauwe staafjes op de bovenste en alle rode op de onderste rij’.

Zo ontdekken de kinderen dat 9 ook als 5 en 4 te zien valt.

Nu worden er ander splitsingen bekeken die tot dan nog met kastanjes gelegd waren.

Nu gaan de kinderen de splitsing zien

binnen de lijnstructuur en als groepjes model; groepjes van 5 vallen extra op, die worden vaker in één kleur gesorteerd.

De rekenstaafjes zijn heel bruikbaar om het lastige aftrekken in het begin van de eerste klas (groep3) concreet te maken.

Er wordt gewerkt binnen het 10-tal met staafjes van één kleur.

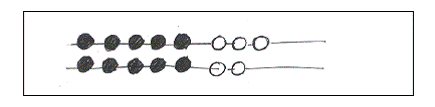
Bij de opdracht 9 eraf 6 plaatsen de kinderen eerst 9 stafjes van de zelfde kleur. ‘Eraf 6’, wordt nu uitgevoerd door 6 staafjes om te draaien en weer in het gaatje te plaatsen.

Anders dan bij het ‘weghalen’ van de af te trekken hoeveelheid, waarbij alleen het ‘antwoord’ zichtbaar wordt, blijft nu het begingetal 9 bestaan en wordt duidelijk hoe de bewerking het getal 9 splitst in 3 en 6.

De activiteiten met het rekenrek zijn gericht op het memoriseren van (reken)feiten tot

20, ze ondersteunen de overgang van structureren naar optellen en aftrekken.

Men hanteert daarbij getalbeelden in een 5 structuur. Kinderen leren eerst de getallen opzetten en herkennen. Begonnen wordt met eenvoudige waarden van 1 tot en met 6.

Nadat die gememoriseerd zijn kan met meer complexe getalbeelden gewerkt worden, bijvoorbeeld de overige getallen tot en met 12, of tot en met alle splitsingen die samen10 zijn. Pas daarna komen ook getalbeelden tot 20 aan bod.

Splitsingen onder de 10 hebben de kinderen in klas 1 (groep 3) met de rekenstaafjes in de gaatjes spelenderwijs geleerd. Op het rekenrek schuiven de meeste kinderen bij de opdracht: ‘Zet er eens 6 op’, in één greep 5 kralen naar links want ze weten al: 6 is 5 en 1. Maar ook werd de 6 herkend als dubbelbeeld: 3 boven en 3 onder.

Zo een geheel splitsen in groepjes leek op het al eerder geoefende structurerend optellen of aftrekken met kastanjes of de damschijven.

Nu kunnen de kinderen het optellen en aftrekken tot 20 op het rekenrek verkennen.

Dat hoeft nog niet in mentale denkbeelden, maar kan langs de gestructureerde weg van het rekenrek-model.

De leerkracht geeft de opdracht: ‘Zet er boven 8 en onder 7 op.’

Als dat gedaan is vraagt ze: ‘Hoevéél zijn dat er eigenlijk samen?’

Dat is niet moeilijk: ‘Vijftien juf ’, roepen de kinderen.

‘Hoe zie je dat zo vlug’, vraagt de leerkracht aan een meisje.

‘Gewoon’, zegt ze, ’10 rode en 3 en 2 witte, dat is 15 bij elkaar.’

Een ander kind is nog bezig met zijn rekenrek, hij schuift:

‘Ik doe het anders juf ’, roept hij, ‘ik doe de 2 er boven bij en onder haal ik ze eraf. Dan zie je zo dat het 3 x 5 is en dat is 15’.

Klassikaal werkend kan op deze manier het gebruik van het rekenrek verkend en geoefend worden.

Sommige kinderen maken snel de sprong naar het mentaal rekenen. Voor hen komt er een moment dat het rekenrek niet meer nodig is. Dat is het lot dat alle concrete rekenmateriaal beschoren is: het maakt zichzelf overbodig. Te lang doorgaan heeft dan een averechts effect en diskwalificeert de innerlijke sprong naar het mentale rekenen

die het kind gemaakt heeft.

Andere kinderen zullen nog lang het steuntje van het rekenrek – of later een ander gestructureerd rekenhulpmiddel – nodig hebben. Het maakt het rekenen veilig en laat altijd ruimte om door te groeien naar een meer mentaal rekenproces.

Het werken met klassikale rekenhulpmiddelen voorkomt dat kinderen heimelijk op hun vingers blijven rekenen, dat soms compenserend door voor hun vingers de kleurpotloden uit hun kleurdoos te nemen als stiekeme visuele zekerheid. Maar altijd één voor één tellend.

In een volgende les is het aftrekken aan de beurt.

‘14 eraf 6’, is de opdracht. Dat kan op twee manieren.

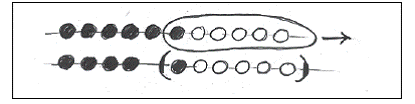
Door er van de bovenste rij 6 weg te schuiven blijft er een dubbel-

4 structuur over. Die getallen kennen de kinderen wel.

Anderen kiezen voor:

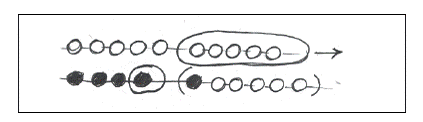
Andere kinderen beginnen bij de onderste rij, waar ze er 4

weg schuiven en dan boven nog 2 eraf:

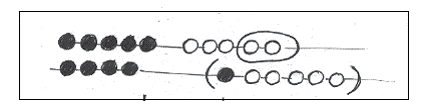
Deze kinderen herkennen daarna in 5 en 3 het 8-beeld. Een enkeling moet dit nog tellend vaststellen, dus vanaf 5 dóórtellend: “6, 7, 8”.

Er treden nu onderling wel grote verschillen op. Het ene kind werkt al snel geheel vanuit voorstellingen. Nienke dekt in de voortgang van de lessen met haar hand een deel van de gaatjes in het deksel van de rekenkist af, verplaatst haar hand zodat er gaatjes afgedekt worden - of juist verschijnen - en leest af wat nu als totaliteit in de structuur van de lege gaatjes te zien is.

Op de vraag van de leerkracht die haar bezig ziet, eens te vertellen wat ze doet, zegt ze: ‘De som is 8 erbij 5. Eerst doe ik dubbel 4 – ze dekt de andere gaatjes met haar hand af- en dan schuif ik er 2 en 2 en 1 bij. Dat is 13, dat zie je zo’.

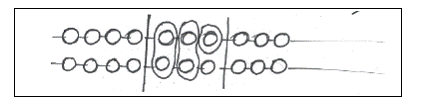
Nienke kan in gedachten al helemaal uit de voeten met verschillende getalbeelden, ze gebruikt de voorstelling van de lege rekengaatjes als een soort mentaal kladblaadje waarop ze haar uitkomsten in haar hoofd ‘als voorstelling’ bij houdt.

Het zal niet lang meer duren of ze heeft ook die voorstelling niet meer nodig.

Bij andere kinderen verloopt dat niet zo vlug, bij hen moet dit denken ‘in modellen’ grondig geoefend worden, voor concreet handelen via de voorstelling daarvan overgaat in het mentale rekenen.

Als de andere kinderen zelfstandig aan het werk zijn, kan de leerkracht de voorzichtige ‘teller’ Martin nog eens extra hulp geven om getalbeelden aan de hand van het rekenrek en voorstellingen daarvan, in te prenten.

Ze gebruikt daarvoor het stapeltje getalkaartjes uit zijn rekenkist en de rekenstaafjes met de gaatjes in het deksel.

‘Zoveel staafjes moet je neerzetten’, zegt de leerkracht.

Ze laat het kaartje met het getal 12 zien. Martin aarzelt even en zegt dan:

’12.’ Hij begint rode staafjes te plaatsen tot hij er 5 heeft. Hij kijkt even naar juf.

Die vraagt: ‘Hoeveel zijn dat er?’ Ze schuift de opengelegde kaartjes naar hem toe. Martin pakt de 5. Hoe ga je nu verder? Hij wijst op de 5 en plaatst nog eens 5 staafjes onder de andere. Hij kijkt voldaan naar juf.

‘Dat zijn er ….?’ ‘10’, zegt Martin stralend. ‘Maar je moest er ….?’

Oei, te vroeg blij geweest: ‘Eh – hij kijkt naar het eerste kaartje dat boven het deksel ligt – 12’ en zet er nog twee staafjes bij: ’11 - 12.

De leerkracht pakt een rekenrek met kralen en vraagt hem nog eens hetzelfde.

Nu schuift hij vlot: 5 – 5 – 2.

‘Kun je met je kaartjes laten zien wat je gedaan hebt?’, vraagt de leerkracht.

Martin begint met de 12 en legt, zoals hij dat ook in zijn schrift getekend en geschreven heeft:

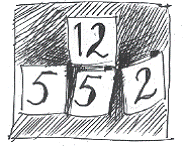
Rekenen op concreet niveau in structuren, die ‘een model VAN’ een

rekenwijze zijn, is dan vervangen door rekenen per 5 met voorstellingen die ‘model VOOR’ zulke berekeningen zijn. Dit bereidt een geautomatiseerd rekenen op basis van rekenfeiten voor.

De leraar die zo eventjes samen oefent, geeft een kind steun door aanschouwelijke

voorstellingen en appelleert aan het visuele geheugen.

Daarbij blijft te bedenken dat rekenen iets is wat je innerlijk doet, iets actiefs, een

mentale handeling waarvan alleen het resultaat, het uiteindelijke antwoord, als voorstelling verschijnt. In het ‘ritmisch rekenen’1 wordt juist dat mentale hándelen ondersteund.

6 Over de rekenkist

De rekenkist is ontwikkeld door de Ontwikkelgroep Rekenen in Beweging, in het bijzonder door Annemieke Zwart vanuit haar ervaringen in het remediërend werken met kinderen met rekenproblemen.

De rekenkist is vorm gegeven door Kees Verhage, uitgevoerd als leermiddel bij Rekenen in Beweging (bronnenboek voor periode onderwijs) en bij de Rekenwerkschriften (leerlingen verbruiksmateriaal, bij het bronnenboek).

Voor het bewaren van het rekenmateriaal van de kinderen bevat de rekenkist vakjes van verschillende vorm en grootte, die deels al gevuld zijn met rekenattributen. Die vakjes zijn afgedekt met het schoolbordje dat omgedraaid dienst kan doen voor het opzetten van kaartjes bij rekenopdrachten en spelletjes.

Het deksel van de rekenkist bevat aan de achterkant het rekenplankje dat de basis vormt voor het didactische materiaal.

Een set rekenattributen is toegevoegd. Dit basismateriaal is ontworpen om op concreet niveau structurerend rekenen en rekenen tot 20.en later tot 100 te ondersteunen.

Voor hogere leerjaren kan de inhoud met in het eigen onderwijs ontworpen leermiddelen aangevuld worden.

De set rekenattributen bestaat uit:

· 20 staafjes voor de rekenholletjes

· Set damschijven voor tellend en structurerend rekenen.

· Set dobbelstenen met cijfers (4-, 6-, 8-, 2x 10-, 12- en 20-vlak).

· 40 grote kralen (10 rood, 10 blauw, 10 wit, 10 bruin).

· 100 kleine kraaltjes (50 wit, 50 bruin)

· Stug rijgdraad en elastisch snoer met knijpertje.

· Sponsje.

· Pak blanco rekenkaartjes (voor spelletjes, getalbeelden, etc.)

7 Aanbevolen literatuur

· Rekenen in Beweging; F. Goffree e.a. SLO/VPC ‘1994.

· Rekenwerkschriften voor de vrijeschool. Annemieke Zwart en

KeesVerhage, Christofoor/Mercurius.

· Rekenwerkschriften in de vrijeschool A. Zwart. Artikel voor Panama

Post (in voorbereiding).

· Rekenen in Beweging voor leraren ouders en studenten; herzien

door Peter Landweer en Annemieke Zwart, Mercurius (in voorbereiding

Duitse en Engelse versie: 2002)

· Rekenspelletjes in de Vrije School. Peter Landweer OOC. Hogeschool

Helicon Zeist, (interne publicatie 2000)

· Het Rekenrek. In Wiskunde&Didactiek 1, F Goffree Wolters-

Noordhoff 1994 p 260ev

· Tussendoelen Anex Leerlijnen, Hele getallen onderbouw Basisschool.

Van den Heuvel Panhuizen ed. Wolters-Noordhoff.